二叉树的那些事

出来混总是要还的，以前算法课睡觉流的口水，如今变成了眼角的泪。学生好好学习比什么都重要 😭😭。

二叉树 (Binary tree)

在计算机科学中，二叉树（英语：Binary tree）是每个节点最多只有两个分支（即不存在分支度大于 2 的节点）的树结构。通常分支被称作“左子树”或“右子树”。二叉树的分支具有左右次序，不能随意颠倒。

二叉树的遍历主要有深度优先、广度优先两类。深度优先根据子节点的访问顺序又分为前序遍历，中序遍历和后序遍历。见下表

遍历方法	遍历顺序	遍历图	备注
前序	根 → 左 → 右		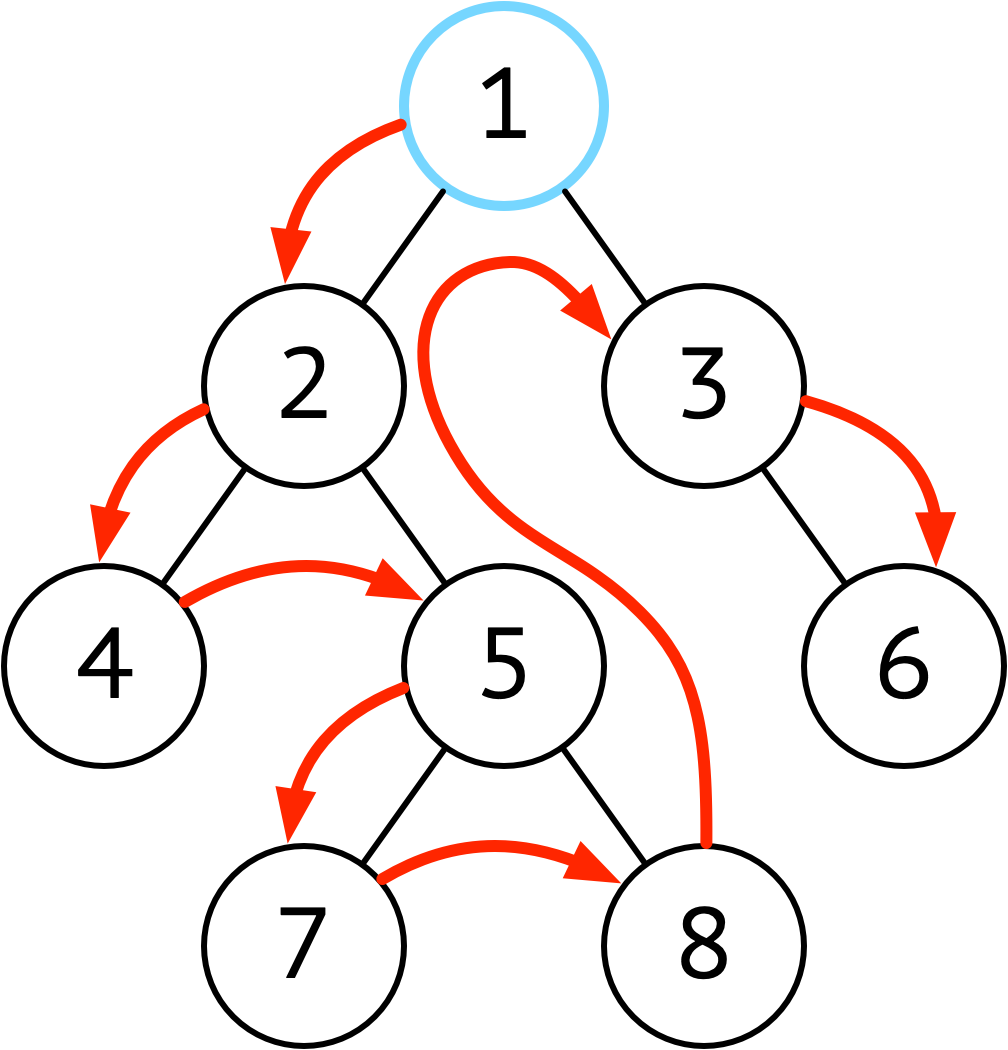前序遍历对当前节点有着最高的处理优先级，能在前序处理掉的逻辑尽量放在前序处理
中序	左 → 根 → 右		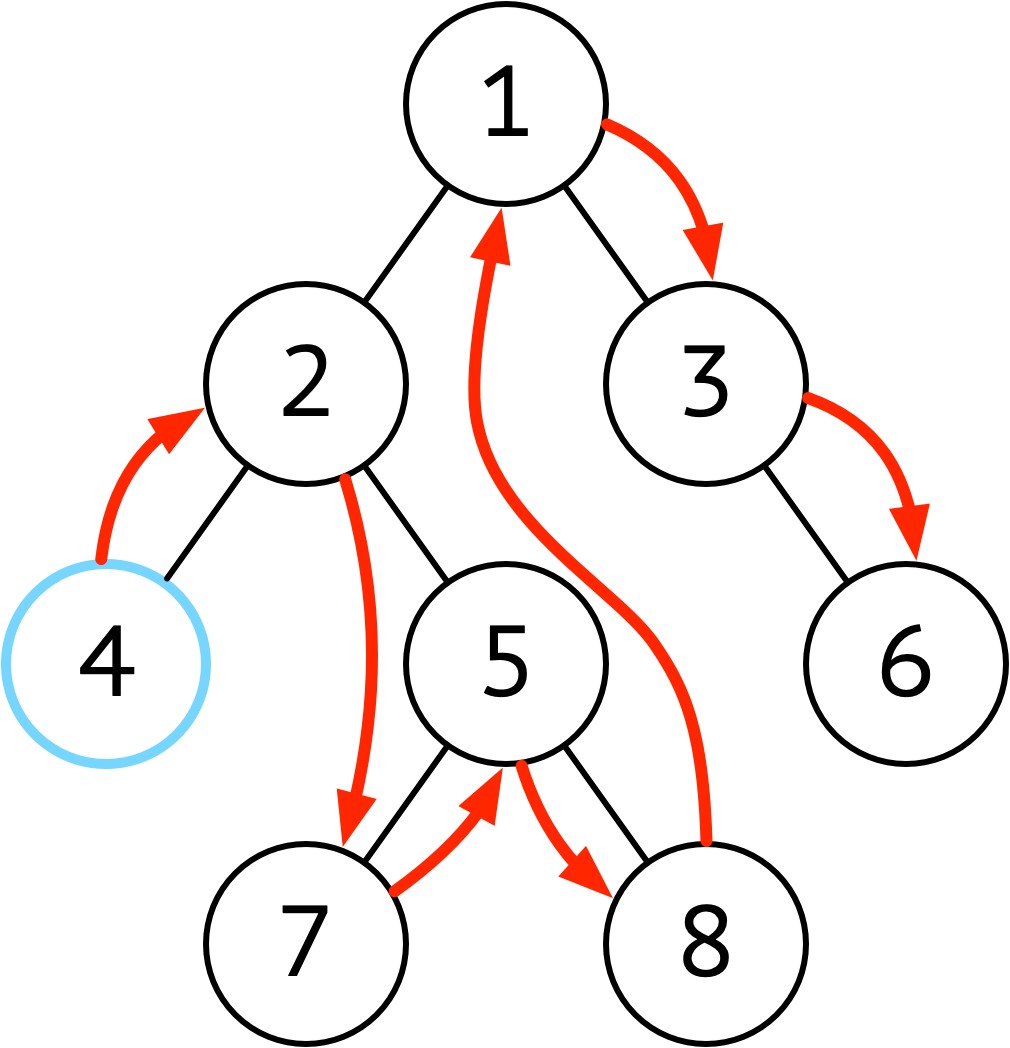中序遍历在二分搜索树 BST 中有用
后序	左 → 右 → 根		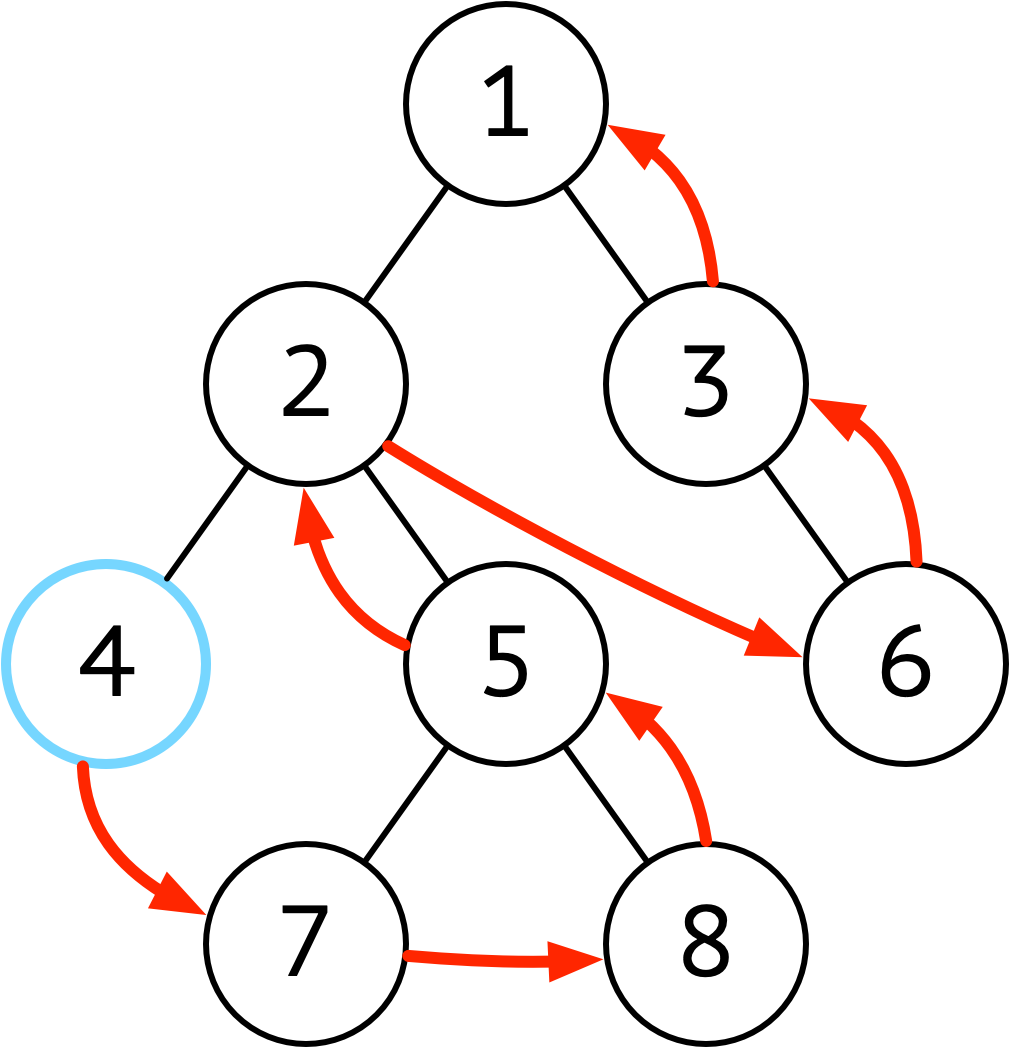后序遍历是左右节点已经遍历完再进行的，因此适合一些收尾工作
广度优先	按深度遍历		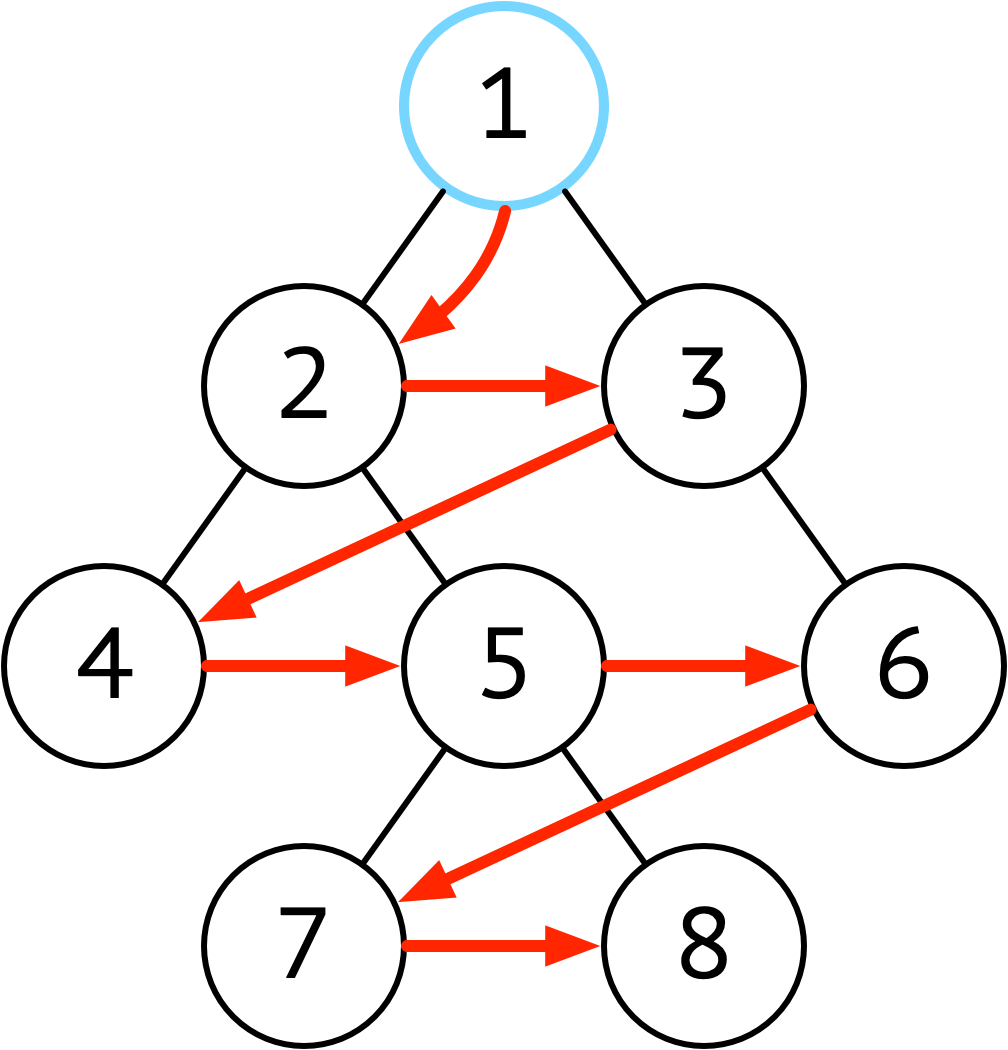深度优先一般用队列实现，用栈也行，关键是要记录每层的遍历任务即可

算法模板

深度优先搜索 Depth-First Search (DFS)

递归

深度优先的算法使用递归有着极其简洁的代码结构，如下，在递归的前后简单插入逻辑即可。

const dfs = (node: TreeNode | null) => {
  if (!node) return;
  // 在递归之前的都属于前序
  dfs(node.left);
  // 遍历完左节点后的属于中序
  dfs(node.right);
  // 左右节点遍历完是后序
};

See the Pen DFS-Recursion by enjoy7ech (@enjoy7ech) on CodePen.

循环

前序遍历

使用循环实现前序遍历需要借助栈，在每次循环依次压入右节点，左节点，每次循环优先出栈的就是左节点了，也就是左子树的根节点。

const preOrder: number[] = []
const dfsPreWithLoop = (node: TreeNode) => {
    // 先压入根节点开启循环
    const stack: TreeNode[] = [node]
    while(stack.length){
        const item = stack.pop()
        // 执行前序逻辑
        preOrder.push(item.val)

        if(item.right) stack.push(item.right)
        if(item.left) stack.push(item.left)
    }
};

See the Pen DFS-Loop by enjoy7ech (@enjoy7ech) on CodePen.

中序遍历

中序遍历比较复杂，依然需要使用栈。因为中序遍历需要先全部获取左子树，因此循环体设计如下

1. 第一步是把当前根节点与左节点一直压栈到叶子节点
2. 然后出栈便实现了左->根的遍历
3. 然后把右节点作为根节点（如果有的话），重复 1.。没有则需要跳过 1.

需要注意的是循环的退出条件，比较容易想到的是栈是否为空，但是整个树的根节点在执行 3.的时候栈是空的，因此还要判断还要加个或者当前根节点是否存在，存在则需要继续压入根节点的右子节点。

const midOrder: number[] = [];
const dfsMidWithLoop = (node: TreeNode) => {
  let p: TreeNode | null = node,
    stack: TreeNode[] = [];
  while (p || stack.length) {
    while (p) {
      stack.push(p);
      p = p.left;
    }
    const node = stack.pop();
    midOrder.push(node.val);
    if (node.right) p = node.right;
  }
};

See the Pen DFS-Loop by enjoy7ech (@enjoy7ech) on CodePen.

后序遍历

后序遍历需要的压栈顺序则是根右左，需要保证在左右节点都访问过了在访问根节点。则可以用哈希表记录下当前节点是否访问过，只有被访问过了才可以出栈。循环结构如下

1. 出栈元素，如果当前元素被访问过则进入后序遍历的逻辑，没访问过则标记为访问过再入栈。
2. 依次入栈当前元素的右左节点（如果存在）。重复 1.

需要注意的是为了启动循环，需要把树的根节点提前压栈。

const sufOrder: number[] = [];
const dfsSufWithLoop = (node: TreeNode) => {
  let visited = new Map<TreeNode, boolean>(),
    stack: TreeNode[] = [node];
  while (stack.length) {
    const node = stack.pop()!;

    if (visited.has(node)) {
      sufOrder.push(node.val);
    } else {
      stack.push(node);
      visited.set(node, true);
      if (node.right) stack.push(node.right);
      if (node.left) stack.push(node.left);
    }
  }
};

See the Pen DFS-Loop by enjoy7ech (@enjoy7ech) on CodePen.

广度优先搜索 Breadth-First-Search (BFS)

队列

提到广度优先通常第一反应就是队列，其实是为了层序的从左到右，本质上还是循环每层的节点并找到下层节点用于下一次循环。因此使用两个栈可以实现层序从右往左的遍历。

const order: number[] = [];
const bfs = (node: TreeNode) => {
  const queue: TreeNode[] = [node];
  while (queue.length) {
    let len = queue.length;
    while (len--) {
      const item = queue.shift();
      order.push(item.val);
      if (item.left) queue.push(item.left);
      if (item.right) queue.push(item.right);
    }
  }
};

See the Pen BFS by enjoy7ech (@enjoy7ech) on CodePen.

Binary Search Tree (BST)

二叉查找树是满足某些条件的特殊二叉树。任何一个节点的左子树上的点，都必须小于当前节点。任何一个节点的右子树上的点，都必须大于当前节点。任何一棵子树，也都满足上面两个条件。另外二叉查找树中，是不存在重复节点的。

二叉搜索树上的基本操作所花费的时间与这棵树的高度成正比。对于一个有 n 个结点的二叉搜索树中，这些操作的最优时间复杂度为$O(log n)$，最坏为 $O(n)$。随机构造这样一棵二叉搜索树的期望高度为$O(log n)$。

搜索

由于 BST 的特殊性质，查找元素的时间复杂度为$O(h)$。

插入

由于 BST 的特殊性质，插入元素的时间复杂度为$O(h)$。

删除

删除分几种情况：

1. 删除的是叶子节点，直接删除。
2. 删除的是链节点（只有左或者右节点），子树直接替代被删节点。
3. 删除的是正常节点，使用前驱（左子树的最大节点）或者后驱（右子树的最小节点）替代被删节点，然后删除该节点。由于前驱节点或后驱节点肯定是链节点前驱的右节点必然为空，否则其右节点才是前驱。同理后驱，所以可以直接走 2.

刷个题： 450. 删除二叉搜索树中的节点

// 由于需要删除节点，我喜欢递归父节点与到当前节点的索引，这样删除直接修改索引即可完成删除。
const deleteInBST = (root: TreeNode, key: number) => {
  const dfs = (
    father: { [key: string]: TreeNode } | TreeNode,
    index: string
  ) => {
    const node = father[index];
    if (!node) return;
    // 找到了需要删除的节点
    if (key === node.val) {
      if (node.left && node.right) {
        // 左右树都存在，寻找后驱，由于需要删除后驱节点，还是采用保存索引的方式。
        let sufLink: [TreeNode, string] = [node, "right"];
        while (sufLink[0][sufLink[1]].left) {
          sufLink[0] = sufLink[0][sufLink[1]];
          sufLink[1] = "left";
        }
        // 被删节点替换为后驱节点
        node.val = sufLink[0][sufLink[1]].val;
        // 删除后驱节点，由于是链节点，直接替换成子树即可
        sufLink[0][sufLink[1]] = sufLink[0][sufLink[1]].right;
      } else if (node.left || node.right) {
        //链节点
        father[index] = node.left || node.right;
      } else {
        // 叶子节点
        father[index] = null;
      }
    }
    if (key < node.val) dfs(node, "left");
    if (key > node.val) dfs(node, "right");
  };
  const warp = { root };
  dfs(warp, "root");
  return warp.root;
};

还有一种比较方便的删除方式，就是把当前节点删了，替换为右子树，左子树挂到后驱节点的左侧。但是这样可能会增加树的高度，对于 BST 来说是不利的。

See the Pen BST by enjoy7ech (@enjoy7ech) on CodePen.

AVL 树

放了防止 BST 的退化（变成链表），产生了 AVL 树，AVL 树是一种平衡二叉树为什么不说平衡二叉查找树，我想是因为做平衡就是为了查找的，不是 BST 还做什么平衡 🤪🤪，得名于其发明者的名字（ Adelson-Velsky 以及 Landis）。其必须满足以下条件

1. 左右子树的高度差小于等于 1。
2. 其每一个子树均为平衡二叉树。
3. 是一个 BST。

刷个题：110. 平衡二叉树

为了保证二叉树的平衡， AVL 树引入了所谓监督机制，就是在树的某一部分的不平衡度超过一个阈值后触发相应的平衡操作。保证树的平衡度在可以接受的范围内。具体就是在每个节点加入一个指标：平衡因子（Balance Factor），即某个结点的左子树的高度减去右子树的高度得到的差值。

树的平衡操作

AVL 树的平衡方法有两种，左旋与右旋。

左旋即是整个树往左旋转，根节点的右节点作为新的根节点，右节点的左子树（根据 BST 可知，根节点<该子树所有值<右节点）挂到原根节点的右索引上。只是一个子树在一个区间上换了个方向挂在区间的另一侧了，因此整个树的 BST 性质不会产生变化。同理右旋。

为什么旋转树可以重新变成平衡二叉树呢？

由于插入或删除树节点才会导致 AVL 失去平衡。所以分为需要平衡的四种情况，这些情况只是最小局部图，并不是树的全貌:

1. LL 型、RR 型
   

2. LR 型、RL 型
   

扩展

B-tree

B 树（英语：B-tree）不是上面的二叉树，是一种自平衡的树，能够保持数据有序。这种数据结构能够让查找数据、顺序访问、插入数据及删除的动作，都在对数时间内完成。

根据 Knuth 的定义，一个 m 阶的 B 树是一个有以下属性的树：

1. 每一个节点最多有 m 个子节点
2. 每一个非叶子节点（除根节点）最少有 ⌈m/2⌉ 个子节点
3. 如果根节点不是叶子节点，那么它至少有两个子节点
4. 有 k 个子节点的非叶子节点拥有 k − 1 个键
5. 所有的叶子节点都在同一层

通常说 B 树都是指代一种类型的树。而当和 B+树之类的变体比较时，Ｂ树则代表了最原初的实现：在它内部节点中存储键值，但不需在叶子节点上存储这些键值的记录。

B 树和 AVL 树的不同之处是：

1. B 树属于多叉树又名平衡多路查找树（查找路径不止两个）
2. 维护平衡的方式不同，B-Tree 的平衡性是通过在插入时进行节点分裂来维护的

将新元素插入到这一节点中的步骤如下：

1. 如果节点拥有的元素数量小于最大值，那么有空间容纳新的元素。将新元素插入到这一节点，且保持节点中元素有序。
2. 否则的话这一节点已经满了，将它平均地分裂成两个节点：
   1. 从该节点的原有元素和新的元素中选择出中位数
   2. 小于这一中位数的元素放入左边节点，大于这一中位数的元素放入右边节点，中位数作为分隔值。
   3. 分隔值被插入到父节点中，这可能会造成父节点分裂，分裂父节点时可能又会使它的父节点分裂，以此类推。如果没有父节点（这一节点是根节点），就创建一个新的根节点（增加了树的高度）。

2–3–4 tree

2-3-4 树（英语：2–3–4 tree）在计算机科学中是阶为 4 的 B 树。2-3-4 树把数据存储在叫做元素的单独单元中。它们组合成节点，每个节点都是下列之一：

1. 2-节点，就是说，它包含 1 个元素和 2 个子节点
2. 3-节点，就是说，它包含 2 个元素和 3 个子节点
3. 4-节点，就是说，它包含 3 个元素和 4 个子节点

Red–black tree

红黑树（英语：Red–black tree）是每个节点都带有颜色属性的二叉查找树 (BST)，颜色为红色或黑色。在二叉查找树强制一般要求以外，对于任何有效的红黑树增加了如下的额外要求：

1. 节点是红色或黑色。
2. 根是黑色。
3. 所有叶子都是黑色（叶子是 NIL 节点）。
4. 每个红色节点必须有两个黑色的子节点。（或者说从每个叶子到根的所有路径上不能有两个连续的红色节点。）（或者说不存在两个相邻的红色节点，相邻指两个节点是父子关系。）（或者说红色节点的父节点和子节点均是黑色的。）
5. 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。

B+树

B+树是在 B 树的基础上又一次的改进，其主要对两个方面进行了提升，一方面是查询的稳定性，另外一方面是在数据排序方面更友好。区别主要在以下几个方面：

1. B 树的节点(根节点/父节点/中间节点/叶子节点)中没有重复元素，B+树有。
2. B 树的中间节点会存储数据指针信息，而 B+树只有叶子节点才存储。
   B+树非叶子节点仅存储指针不存储数据，这样一个节点就可以存储更多的指针（这里个人理解是数据的索引比节点指针大），可以使得 B+树相对 B 树来说更矮，所以查询速度更快。
3. B+树的每个叶子节点有一个指针指向下一个节点，把所有的叶子节点串在了一起，形成一个有序链表。

---

2024-05-21

还原树算法

105. 从前序与中序遍历序列构造二叉树

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {number[]} preorder
 * @param {number[]} inorder
 * @return {TreeNode}
 */
var buildTree = function (preorder, inorder) {
    let cur = 0
    const buildTree = (left, right) => {
        if (cur < 0 || cur >= preorder.length) return
        const inId = inorder.findIndex(o => o === preorder[cur])
        const node = new TreeNode(preorder[cur++])
        if (inId > left) {
            node.left = buildTree(left, inId - 1)
        }
        if (inId < right) {
            node.right = buildTree(inId + 1, right)
        }
        return node
    }
    return buildTree(0, preorder.length - 1)
};

记录题解: 主要是循环的思路比较复杂

2024-07-05

二叉树的直径问题

定义：二叉树的直径是指树中任意两个节点之间最长路径的长度。这条路径可能经过也可能不经过根节点root。
两节点之间路径的长度由它们之间边数表示。

思路其实就是在后序遍历时，已知当前节点的左右子树深度，相加便能得到该节点为根节点的最长链，最后取最大值。
Q: 以所有节点为根节点的最长链覆盖的解空间，是否必然包含直径?
A: 直径必然会经过一个根节点，因此是个充要条件。

543.二叉树的直径

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var diameterOfBinaryTree = function (root) {
    let ans = 0
    const dfs = (node) => {
        if (!node) return 0
        const l = dfs(node.left)
        const r = dfs(node.right)
        ans = Math.max(ans, l + r)
        return Math.max(l, r) + 1
    }
    dfs(root)
    return ans
};

二叉树经过特定节点的最长路径问题

如果指定一个节点，求经过该节点的最长路径呢？

问题应该分为两部分：

1. 求该节点为根节点的子树的深度。
2. 删除该节点的孩子，求经过该叶子节点的最长链。

小技巧：

由于求解的是子树深度，所以肯定是后序遍历。
在未遍历到目标节点时，dfs利用负数作为递归返回值做节点深度。
在遍历到目标节点时，此时可以求解到问题1的解（负数转正）。
此时不再返回该节点（也就是目标节点）的深度，而是进入求解问题2的流程，假设已经删除该节点的孩子，并返回正数深度1。
因此，递归在返回时需要判断左孩子深度与有孩子深度是否有正数，有正数说明目标节点在正数子树那一侧。并且在返回之前更新最终解，也就是：问题1的解+左子树深度的绝对值+右子树深度的绝对值（因为有可能有负数深度）。

留一道变种题。2385. 感染二叉树需要的总时间