在计算机被日益依赖的今天,数学计算越来越依赖计算机,但是我告诉你在计算机中0.1+0.2不等于0.3,你会有什么反应呢?
一般可能会说WTF?🧐确实。今天俺就扒开计算机,看看科学家究竟是怎么设计的浮点数。
计算机里的运算
大家都知道计算机是使用二进制运算的,但是这是为什么呢,是十进制不香吗?这个问题有点欲哭无泪。可以联想到有人把计算机扒开,揪出里面的工作人员大声吼他:为什么不用十进制!嗯。。。
其实计算机里是一堆电路,是使用高低电平表示01的,然后经过一堆电路来进行运算的。比如说两根导线,一根有电,一根没电,经过了一个节点输出一个电平他就完成了一个运算,这个节点一般被称为逻辑门,一般是用二极管实现的。
使用逻辑门就能实现与或非的运算,再经过复杂的组合就可以使得二进制的数(在计算机里是一堆电信号)完成整个世界庞大的代数系统运算。这个电路图的设计在当代社会有个响当当的名字:芯片。当然芯片不只是负责运算的,运算单元只是其中的很小一部分。
负数的表示方式
二进制只有01,如何表示负数是最先需要定义的,很简单也很符合直观的,第一位是0,那就是正数,第一位是1,那就是负数。
对于加法器(芯片中负责加法运算的单元)来说,这样的设计对其做出了设计要求:需要识别负数,并作出正确的逻辑处理。
通常不会实现专门的减法器,而是通过先将操作数取负然后执行加法来实现减法操作。这种设计使得硬件更加简洁和高效,同时保持了对不同数据类型和操作数的通用性和灵活性。
反码与补码
负数定义好了,怎么正确处理加法运算呢?
二进制数的反码(1’s complement)是指将二进制数每个数字反转得到的数:若某一位为0,则使其变为1,反之亦然。
如果进行反码运算时,正数使用原码,负数使用反码除符号位,情况如:-2+3 = 1010 + 0011
就会变成1101(反) + 0011(反) = 0000(反),这与正确结果差了1。那自然会联系到在负数转反码后对他再加1,这也恰好等于补码(2's complement)。使用补码即可正确的完成负数的加法运算。原理可以参考补码的工作原理。-2+3 = 1110(补) + 0011(补) = 0001(补)就可以得到正确的结果,可以发现结果是出现了上溢,补码也正是利用了上溢的值有部分等价的属性。
浮点数的表示方式
换个角度看看我们日常使用的十进制数,比如10.25: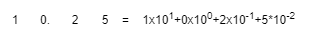
换成二进制这是同样的道理,所谓浮点数,就是小数点是会浮动的数,也就是2的0次方在偏移。这种方式十分利于在计算机中实现。
由于芯片不可能无限制的增加针脚,并且芯片的设计、指令集以及配套的系统设计很复杂,这就产生了处理器位数的限制,现在比较常见的一般是32位与64位处理器芯片。这就意味着想要做运算,单次最长只能输入64位/32位的二进制数。想要用64位二进制数完成包含小数在内的所有数字表示以及运算,这对工程师提出了挑战。
IEEE 754
在六、七十年代,各家计算机公司的各个型号的计算机,有着千差万别的浮点数表示,却没有一个业界通用的标准。这给数据交换、计算机协同工作造成了极大不便。IEEE电机电子工程师学会是一个建立于1963年1月1日的国际性电子技术与电子工程师协会,亦是世界上最大的专业技术组织之一,拥有来自175个国家的42万会员。的浮点数专业小组于七十年代末期开始酝酿浮点数的标准。在1980年,英特尔公司就推出了单片的8087浮点数协处理器,其浮点数表示法及定义的运算具有足够的合理性、先进性,被IEEE采用作为浮点数的标准,于1985年发布。而在此前,这一标准的内容已在八十年代初期被各计算机公司广泛采用,成了事实上的业界工业标准。加州大学伯克利分校的数值计算与计算机科学教授威廉·卡韩被誉为“浮点数之父”。
IEEE二进制浮点数算术标准(IEEE 754)是20世纪80年代以来最广泛使用的浮点数运算标准,为许多CPU与浮点运算器所采用。看来只要参透了这个标准,0.1+0.2的问题就会得到答案。
表示方式
IEEE 754规定了四种表示浮点数值的方式:单精确度(32位)、双精确度(64位)、延伸单精确度(43比特以上,很少使用)与延伸双精确度(79比特以上,通常以80位实现)。只有32位模式有强制要求,其他都是选择性的。
与整数的表示方式类似,第一位是符号位。然后划分几个比特位用来存储移位,小数点可以往左也可以往右。最后剩下的比特位用于存储数字部分。

移码(阶码)
符号位无需多说,先看指数部分exponent,指数部分如果采用第一位也是符号位的设计,在比较大小时,就会比较麻烦,还会有+0与-0的问题。因此,在计算机科学中,移码(英语:Offset binary)是一种将全0码映射为最小负值、全1码映射为最大正值的编码方案。就相当于把二进制数往负方向整个平移一部分,n比特的二进制数的这个平移量规定为。
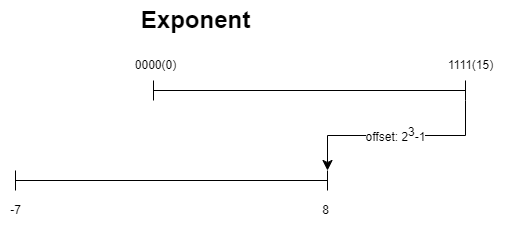
这么设计十分利于大小的比较,直接从第一位往后比较即可。特别的是,指数部分的全0与全1被用作特殊值处理。特殊值在下面会介绍。
规约形式的浮点数
有了移码的设计,还不能规约一个数的表示,例如十进制的10.25,可以表示为1.025e1(小数点往右移动一格),也可以表示为0.1025e2,这样比较大小很不方便。
为了解决这个问题,需要对浮点数做规约化。其实十分简单:就是科学记数法。科学记数法是把一个数表示成a与10的n次幂相乘的形式(1≤|a|<10,a不为分数形式,n为整数)例如:,把10换成2就是浮点数的规约化。
如,这么表示有一个明显的前提:那就是第一位必须是1,为了与二进制科学计数法的尾数(mantissa)相区别,IEEE754称之为有效数(significant)。特别的是,有效数在存储时首位1是省略的,那就是为什么双精确度(64位)浮点数的有效数只有52位,但是能表示的最大数却是。
非规约形式的浮点数
如果浮点数的指数部分的编码值是0,有效数部分非零,那么这个浮点数将被称为非规约形式的浮点数。一般是某个数字相当接近零时才会使用非规约型式来表示。也就是上文说的特殊值之一。
IEEE 754标准规定:非规约形式的浮点数的指数偏移值比规约形式的浮点数的指数偏移值小1。
例如单精度的浮点数,指数部分是8个比特位,指数部分全0时,理论上实际的偏移值为。但是由于标准规定,所以非规约形式的浮点数的偏移值为-126,与规约形式的指数1对应的实际偏移值是一样的。
这么设计的原因是70年代末IEEE浮点数标准化专业技术委员会酝酿浮点数二进制标准时,Intel公司对渐进式下溢出(gradual underflow)的力荐。当时十分流行的DEC VAX机的浮点数表示采用了突然式下溢出(abrupt underflow)。
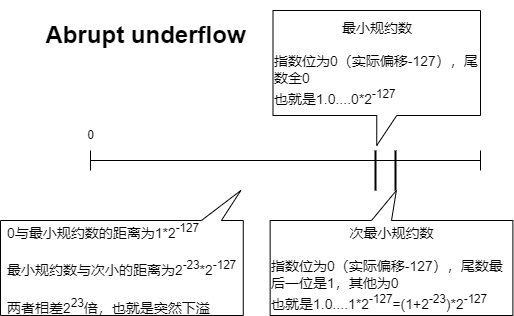
而使用Intel公司的渐进式下溢出,情况是这样的
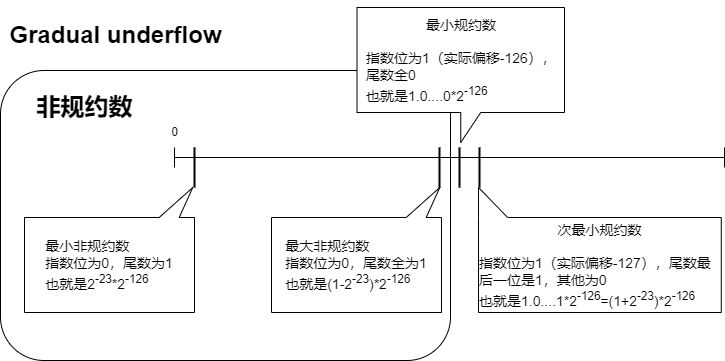
指数位的特殊值
非规约形式利用了指数位为0进行特殊处理,下列的这些情况,也属于类似的处理,以单精度浮点数为例:
| 指数 | 实际偏移 | 有效数 | 备注 |
|---|---|---|---|
| -127 | 全0 | 有效数部分全为0代表0 | |
| -127 | 不为全0 | 实际小数为大于0小于1,有效数部分省略首位0,属于非规约数区间 | |
| ~ | -126~127 | 没有限制 | 实际小数为大于等与1小于2,有效数部分省略首位1,属于规约数区间 |
| 128 | 全0 | 代表无穷,配合符号位代表正负无穷大 | |
| 128 | 不全为0 | 代表NaN,是非法的数 |
舍入规则
任何有效数上的运算结果,通常都存放在较长的寄存器中,当结果被放回浮点格式时,必须将多出来的位数丢弃。有多种方法可以用来执行舍入作业,实际上IEEE标准列出4种不同的方法:
舍入到最接近:舍入到最接近,在一样接近的情况下偶数优先(Ties To Even,这是默认的舍入方式):会将结果舍入为最接近且可以表示的值,但是当存在两个数一样接近的时候,则取其中的偶数(在二进制中是以0结尾的)。
朝+∞方向舍入:会将结果朝正无限大的方向舍入。
朝-∞方向舍入:会将结果朝负无限大的方向舍入。
朝0方向舍入:会将结果朝0的方向舍入。
浮点运算
在浮点数运算中,根据指数位将尾数对齐是非常重要的步骤。IEEE 754标准中描述了浮点数的表示方式,其中指数部分用于表示数值的大小,尾数部分则包含数值的精度信息。当进行浮点数运算时,如果两个数的指数部分不相等,就需要将它们的尾数对齐,以便进行有效的运算。
根据IEEE 754标准,当对两个浮点数进行加法或减法等运算时,首先需要对这两个数的指数进行比较,如果它们不相等,就需要将指数较小的数的尾数向右移动,使得两个数的指数相等,因此精度越高的数在进行运算时尾数就越有可能在尾数对齐时被舍弃。
0.1 + 0.2
现在再回来看这个问题,假设使用单精度浮点数,那么第一步就是规约化。
对于浮点数的十进制转二进制,还是可以通过类比的方法进行思考。如十进制的10.25如果我们知道小数部分是0.25,怎么取首位2呢?很简单,乘以10取2.5的整数部分即可。
那二进制的0.1,我们如法炮制乘2取整数位,可以发现,这个步骤进入了一个死循环,最终,由于有效数有位数限制,所以0.1在规约的时候会丢失精度。
以单精度的浮点数为例:
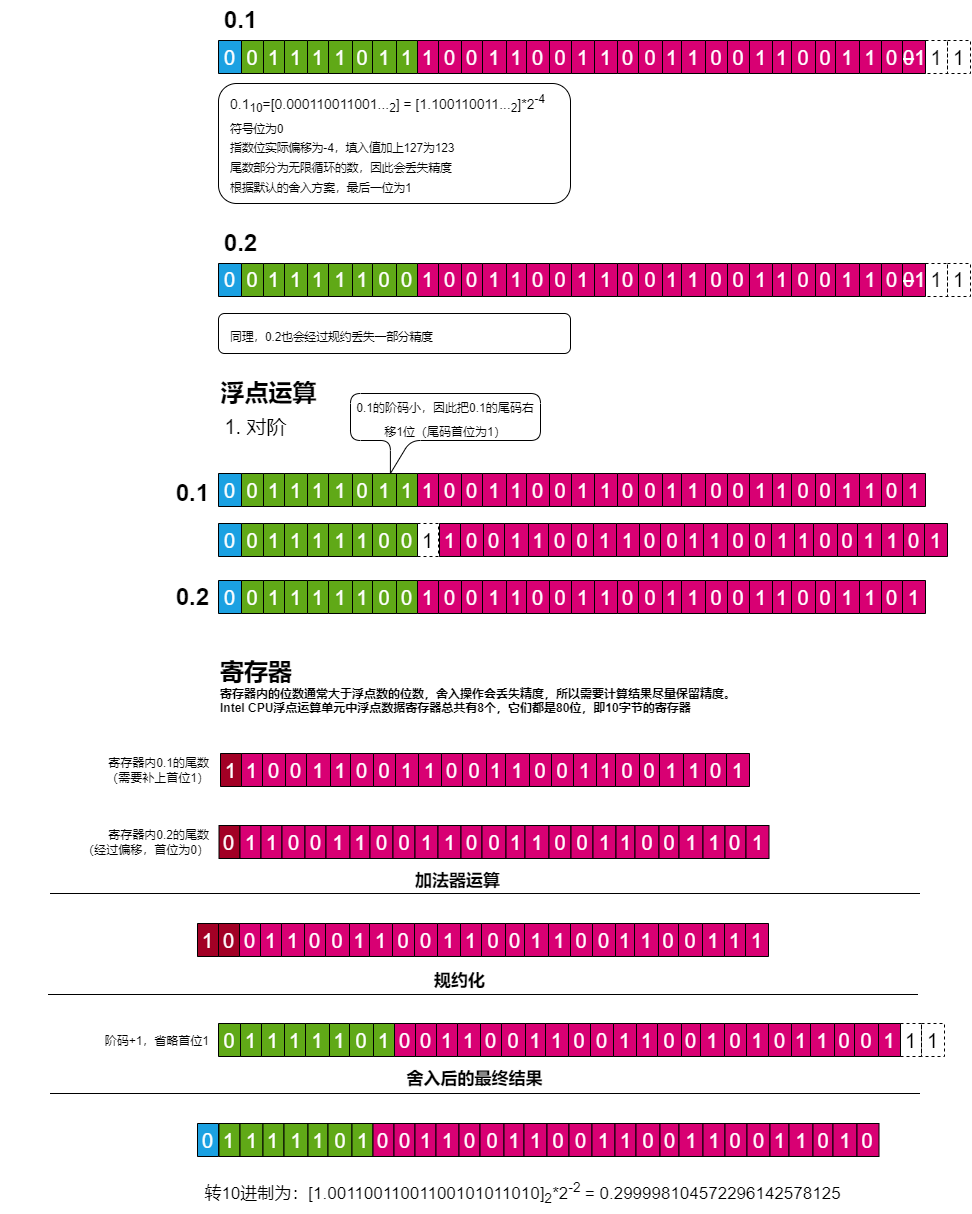
实际上,在采用IEEE754标准的语言中,由于没有无限小数的表示方法,因此十进制的小数使用IEEE754基本没有精准表示。更不用想运算后的结果了,至于程序里为什么有的时候浮点数相加又是正确的结果,这是因为编程语言实现二进制数打印时做了处理。如果不处理,0.1打印出来应该是0.100000001490116119才对。
0.1+0.2这种事情看清原理就像十进制与二进制两个世界的人在沟通时,十进制世界的人(甲方)对二进制世界的人(乙方)说:帮我算个0.1+0.2。其实乙方根本不懂甲方的需求,毕竟二进制的0.1是个无限循环小数。只能依葫芦画瓢的整个0.1,最后算个结果给甲方,甲方使用他们程序员开发的翻译软件翻译出个0.30000000000000004最后被甲方老总臭骂一顿。殊不知程序员为了让0.1+0.1=0.2已经写了好几天代码。
果然沟通才是这个世界最大的误差。
直到现在,工程师仍在为如何合理打印浮点数而努力Printing Floating-Point Numbers。现在不少语言使用的应该是R. G. Burger and R. K. Dybvig于1996年发表的算法,核心思想是使用一种称为“双精度调整”的技术,通过这种技术可以快速确定浮点数的十进制表示,同时确保结果的正确舍入。
